Yellowpaper (Outdated)
April 5, 2022 · 79 minute read

Staking & Unstaking
Staking and unstaking are the basic mechanisms that allow ships to enter and exit gameplay. While ship traits are preserved across stakes and unstakes, unstaking a ship erases its internal travel and banking state. As such, ships may only unstake when they have arrived at The Citadel.
To stake a ship , a pilot sends a transaction including its unique identifier. After verifying that the pilot owns , we map 's unique identifier to the pilot's address, initialize its travel state, and transfer ownership of to the game contract, following the checks-effects-interactions pattern. This is standard practice, and ensures that we know which pilot owns , that 's state is correct from the beginning, and that the pilot may not trade while playing. Unless stated otherwise, every action dependent on a ship is only allowed for its staking pilot.
To unstake , a pilot sends a similar transaction including 's unique identifier. After verifying that the ship is staked, that it belongs to the pilot, and that it is targeting and has arrived at The Citadel, we delete its internal travel and staking state, then transfer it back to the pilot.
Ship Reveals
When a pilot mints a ship, it has no data associated with it. To ensure that ship traits are distributed fairly, each pilot must initiate a reveal for their ship, which pulls a random from Chainlink VRF and uses it as a seed for trait generation. Because all reveals happen on Layer 2, per-request randoms are viable, and each pilot can choose to reveal their ship at any time after mint, instead of having to wait for a batch of seeds.
To accommodate the push-based nature of VRF, ship reveals happen in three stages. First, a pilot sends a transaction to initiate the reveal. During this stage, we check that the ship's trait batch has been validated successfully, the ship has not already been revealed, the pilot owns their ship, and no other reveals are in progress for it. Once the checks are complete, we mark that a reveal is pending for the ship and request a random from Chainlink VRF, which will function as the seed for the ship's traits.
After 30 blocks (roughly 1 minute), the random oracle calls back into the ship traits contract, providing the random number and the ship ID for which it is relevant. In response, we record the random, and note that the ship is ready for reveal.
Once the pilot is notified that their ship is ready for reveal, they may send a final transaction to complete the reveal and assign their ship its traits. During the reveal transaction, we check that the seed exists and that the ship hasn't already been revealed, mark it as revealed, then select and assign its traits.
For all reveals, we use A. J. Walker's alias method to select each ship's independent traits (size, class, designation, hull) and upgrade tiers according to the proper probability distribution. From this information, we are able to fill in the ship's dependent traits (speed, fuel efficiency, reactor, power) without pulling additional randoms. For more information on the distribution of genesis ship traits, see the ship traits section.
Trait Batches
To reduce the number of privileges that the core team must retain, we've created a single ship traits contract that is capable of handling all reveals. In order to consistently apply trait probability distributions across collections of varying size, we have designed a trait batching system. Each trait batch controls a contiguous range of tokens and defines which traits are available for selection, as well as the probability distribution among sets of traits.
Because the collection of selectable traits may be arbitrarily large for each batch, and because it is not possible to validate aliases without knowing the number of selectable traits, we have split the batch preparation process into three stages: creation, uploads, and validation.
The Ships Uploader Role
Ships' traits have a direct impact on the economy, making it critical that they are controlled by either contracts or entities
with economic incentive to behave well. To ensure that this is the case, we have added access control to the ship traits
contract. Batch creation, trait uploads, and trait validation may only be performed by holders of the SHIPS_UPLOADER_ROLE.
Following the pattern we've used for our other contracts, SHIPS_UPLOADER_ROLE is governed by DEFAULT_ADMIN_ROLE.
At launch, SHIPS_UPLOADER_ROLE will be retained by the both the core team and governance. However, DEFAULT_ADMIN_ROLE
will only be retained by governance, allowing the community to remove or replace the core team if necessary.
Creating Batches
When a ship uploader submits a transaction to create a trait batch, they provide a numerical ID for the batch, the range of token IDs that the batch will control, the maximum number of officer trait combinations that can be selected through the batch, and the probability that an officer trait combination will be selected in each reveal.
Before creating the batch, we check that the batch's ID and token range immediately follow those of the previous batch (beginning at 1) and that there is at least one revealable officer trait combination if the officer probability is nonzero.
We then associate all of the provided parameters with the batch's ID and mark that it has entered the Uploading phase.
Ship Uploads
In order to make traits selectable through a batch, a ship uploader submits an upload transaction and includes the batch's ID, a list of trait combinations selectable for officer ships, a list of trait combinations selectable for non-officer ships, a list of corresponding rarity-alias pairs for the non-officer trait combinations, and a flag that indicates whether this will be their final upload.
Without knowledge of the full trait combination lists, we do not have enough information to validate the aliases or
officer ships. As such, we only check that the batch is in the Uploading state, and that there are exactly the same
number of rarities, aliases, and non-officer trait combinations.
Once these checks pass, we add the officer trait combinations, non-officer trait combinations, and rarity-alias pairs to
the batch's state. If the uploader has indicated that this is their final upload, we mark the batch as Validating.
Otherwise, the batch remains in the Uploading state and the uploader may upload additional trait combinations.
Data Validation
Because the collection of selectable trait combinations may be arbitrarily large, we allow for validation to happen in multiple steps, if necessary. To validate a portion of a batch's trait combinations, a ship uploader submits a validation transaction and includes the batch's ID and the number of items to validate in each list.
After checking that the batch is in the Validating state, we resume validation from the first trait combination that hasn't
yet been validated.
If this is the very first trait combination, we start by performing the checks that do not depend on list items: that there is at least one non-officer trait combination available, and if this batch has a nonzero officer probability, there is at least one officer trait combination available.
Either way, we proceed to check that each officer and non-officer trait combination in range is valid (i.e., that each of
its fields is defined), and that each alias is a valid index within the list of non-officer trait combinations. If any of
these checks fail, we immediately stop, delete all of the batch's uploads, return the batch to the Uploading state,
and emit the index of the first offending value.
If we do not encounter any validation issues, we record the index of the last trait combination that we validated. If this
is the final index of the batch, we mark the batch as Ready for reveals, delete all validation-specific state to
conserve gas, and emit an event indicating that the batch is ready for use. Otherwise, the batch remains in the
Validating state and the uploader may validate the next portion.
Ship Traits
Each ship has four traits that correspond to gameplay mechanics: speed, fuel efficiency, reactor cost, and power.
Speed is the number of units that a ship can travel per second. Fuel efficiency and reactor cost determine the travel cost that a ship's pilot pays to seek new opportunities. Fuel efficiency is measured in units per full ore, and reactor cost is a flat fee per travel, measured in ore. Speed, fuel efficiency, and reactor cost are especially relevant to travel, and are covered in depth in the travel section.
In rough terms, a ship's power determines its ore gathering capability. For miners, this is the ship's drill rate, which measures the drill that they accumulate per second during their mining operations. For a fixed ore type and mining duration, this is directly proportional to the ore that they gain. For marauders, this is the ship's attack power, which dictates the percentage of stolen ore it receives, relative to other marauders at its belt. The impact of power is covered in depth for miners in the mining section and for marauders in the roaming section.
tl;dr: For power, travel speed, and fuel efficiency, higher numbers mean that the ship is better suited for the corresponding mechanic. For reactor cost, lower is better, especially for short-distance travel.
For simplicity, classes are referenced by their sizes. Small ships correspond to frigates and interceptors, medium ships correspond to barges and cruisers, and large ships correspond to command ships and battleships.
Each of the tables below corresponds to a ship designation. Ship stats increase based on their designation, and to balance this, the likelihood of ships being these designations varies. Upon reveal, a ship has a 60% chance of being standard, a 30% chance of being noble, and a 9% chance of being exodus.
Standard
| Class | Power | Travel Speed (un/s) | Reactor Cost (ORE) | Fuel Efficiency (un/ORE) |
|---|---|---|---|---|
| Small | 650 | 800 | 2 | 400,000 |
| Medium | 825 | 600 | 6 | 275,000 |
| Large | 1000 | 500 | 10 | 200,000 |
Noble
| Class | Power | Travel Speed (un/s) | Reactor Cost (ORE) | Fuel Efficiency (un/ORE) |
|---|---|---|---|---|
| Small | 850 | 1200 | 2 | 400,000 |
| Medium | 1150 | 1000 | 6 | 275,000 |
| Large | 1400 | 700 | 10 | 200,000 |
Exodus
| Class | Power | Travel Speed (un/s) | Reactor Cost (ORE) | Fuel Efficiency (un/ORE) |
|---|---|---|---|---|
| Small | 1450 | 1600 | 2 | 400,000 |
| Medium | 1650 | 1400 | 6 | 275,000 |
| Large | 1800 | 1200 | 10 | 200,000 |
Standard Upgrades
While noble and exodus class ships have better traits by default, standard ships have a small chance to get upgraded stats upon initial mint. Out of all standard ships minted, 2% will have tier 1 systems, 1% will have tier 2 systems, and 0.5% will have tier 3 systems. More information on upgrades and the meaning of tiers will be outlined in the upgrades section.
| Tier | Class | Power | Travel Speed (un/s) | Reactor Cost (ORE) | Fuel Efficiency (un/ORE) |
|---|---|---|---|---|---|
| T1 | Small | 682.500 | 880 | 1.66 | 420,000 |
| Medium | 886.875 | 645 | 5.5 | 288,750 | |
| Large | 1100.000 | 525 | 9.25 | 210,000 | |
| T2 | Small | 715.000 | 960 | 1.33 | 440,000 |
| Medium | 948.750 | 690 | 5 | 302,500 | |
| Large | 1200.000 | 550 | 8.5 | 220,000 | |
| T3 | Small | 747.500 | 1040 | 1 | 460,000 |
| Medium | 1010.625 | 735 | 4.5 | 316,250 | |
| Large | 1300.000 | 575 | 7.75 | 230,000 |
Ship Naming
When a pilot has accumulated enough ore, they can choose to spend 1000 ore to give their ship a name. After accumulating sufficient ore, pilots may choose to name their ships for vanity purposes. These names are permanent, unique, and displayed prominently in token metadata. To prevent abuse, ships may consist only of alphanumeric characters and spaces. To ensure that existing names stay in sync for the uniqueness check, ships may only be named from Layer 2.
When a pilot submits a transaction to name their ship, we check that the ship has not yet been named and that no other ship's name has the same hash. We then set the ship's name, mark the name's hash as used, and burn 1000 ore from the pilot's account. When pilots move their ships between networks, the ships' names are sent and applied through the dock.
Upgrades
Each ship can be upgraded to increase its power, speed, and fuel efficiency stats, and upgrades are organized by tiers from one to five. Each of the upgrade tiers takes a different amount of time and ore to complete, where time is measured in days. Independent of its tier, every upgrade's time and ore cost differs depending on the ship's class and designation. As in ship traits, classes are written as their sizes: small, medium, and large.
Power Upgrades
| Tier | Class | Ore Cost (Miner) | Ore Cost (Marauder) | Upgrade Time (Days) | Stat Bonus |
|---|---|---|---|---|---|
| T1 | Small | 250 | 500 | 0.25 | 105% |
| Medium | 250 | 500 | 0.25 | 107.5% | |
| Large | 250 | 500 | 0.25 | 110% | |
| T2 | Small | 500 | 1000 | 0.5 | 110% |
| Medium | 500 | 1000 | 0.5 | 115% | |
| Large | 500 | 1000 | 0.5 | 120% | |
| T3 | Small | 1000 | 2000 | 1 | 115% |
| Medium | 1000 | 2000 | 1 | 122.5% | |
| Large | 1000 | 2000 | 1 | 130% | |
| T4 | Small | 2000 | 4000 | 2 | 120% |
| Medium | 2000 | 4000 | 2 | 130% | |
| Large | 2000 | 4000 | 2 | 140% | |
| T5 | Small | 3000 | 8000 | 3 | 125% |
| Medium | 3000 | 8000 | 3 | 137.5% | |
| Large | 3000 | 8000 | 3 | 150% |
Propulsion Upgrades
| Tier | Class | Ore Cost (Miner) | Ore Cost (Marauder) | Upgrade Time (Days) | Speed Bonus | Fuel Efficiency Bonus | Updated Reactor Cost (ORE) |
|---|---|---|---|---|---|---|---|
| T1 | Small | 125 | 200 | 0.125 | 110% | 105% | 1.66 |
| Medium | 125 | 200 | 0.125 | 107.5% | 105% | 5.5 | |
| Large | 125 | 200 | 0.125 | 105% | 105% | 9.25 | |
| T2 | Small | 250 | 400 | 0.25 | 120% | 110% | 1.33 |
| Medium | 250 | 400 | 0.25 | 115% | 110% | 5 | |
| Large | 250 | 400 | 0.25 | 110% | 110% | 8.5 | |
| T3 | Small | 500 | 1000 | 0.5 | 130% | 115% | 1 |
| Medium | 500 | 1000 | 0.5 | 122.5% | 115% | 4.5 | |
| Large | 500 | 1000 | 0.5 | 115% | 115% | 7.75 | |
| T4 | Small | 1000 | 2000 | 1 | 140% | 120% | 0.75 |
| Medium | 1000 | 2000 | 1 | 130% | 120% | 4 | |
| Large | 1000 | 2000 | 1 | 120% | 120% | 7 | |
| T5 | Small | 1500 | 4000 | 2 | 150% | 125% | 0.5 |
| Medium | 1500 | 4000 | 2 | 137.5% | 125% | 3.5 | |
| Large | 1500 | 4000 | 2 | 125% | 125% | 6.25 |
Cost Modifiers
| Class | Designation | Upgrade | Ore Cost Modifier | Upgrade Time Modifier |
|---|---|---|---|---|
| Small | Noble | Power | 115% | 110% |
| Propulsion | 130% | 110% | ||
| Exodus | Power | 160% | 150% | |
| Propulsion | 140% | 130% | ||
| Medium | Noble | Power | 130% | 120% |
| Propulsion | 130% | 110% | ||
| Exodus | Power | 180% | 150% | |
| Propulsion | 160% | 130% | ||
| Large | Noble | Power | 145% | 120% |
| Propulsion | 130% | 115% | ||
| Exodus | Power | 200% | 150% | |
| Propulsion | 180% | 140% |
Calculator
Disclaimer: this calculator uses JavaScript floating point math, instead of the fixed-point representation that we use in Solidity. As such, the results may be ever so slightly different in-game. Please use this calculator to get a feel for the mechanic, then consult the game UI to finalize your decisions.
System
Ship
Target
Travel
Definitions
- - The speed of ship (in units per second)
- - The reactor cost of ship (in ore wei)
- - The fuel efficiency of ship (in units travelable per ore)
- - The current coordinates of ship
- - The Euclidean distance function
Overview
The Citadel's map is a 16:9 rectangle, and points are represented with standard cartesian coordinates. To keep manipulation straightforward from Solidity, coordinates start at and increase from the top left corner of the map, meaning that and for any point are always zero or positive. Aside from the ships docked there, The Citadel is the unique game element with coordinates .
Ship Positions
During gameplay, ships may travel between locations on the map. Because it is impossible to trigger transactions directly from within a contract, we cannot update ships' positions periodically. Instead, we store a ship 's intent to travel as , the coordinates of when the intent was signaled, , the coordinates that is targeting, and , the epoch time at which the signaled its intent.
Logically, we assume that ships travel in a straight line from their last committed coordinates to their target . To compute the position of at epoch time , we first compute the distance it has traveled, . If , we know that the ship has arrived, and that its coordinates are . This technique also serves as a function, preventing overshoots. Otherwise, we know that the ship has not arrived. In this case, because the ship is travelling in a straight line, we can compute its coordinates as . To prevent underflow, each component becomes , and when and , respectively.
Travel Transactions
When initiating a travel transaction for a ship, a pilot includes the ship's identifier and the identifier of the point that they're targeting. After verifying that the pilot has the correct permissions and that the target exists, we can look up and compute . We then commit the ship's current position , note the time , and update the ship's target . Note that because we've placed The Citadel at , each of the values assigned here is automatically correct before initialization (i.e., the first travel transaction), due to the EVM's zero defaults.
After we've updated the ship's travel state to reflect its intent, we compute and transfer the ore necessary to get there. Fuel cost in ore for each trip is simply the distance the ship will travel, divided by the ship's fuel efficiency, plus the ship's reactor cost, given as . Because native fixed-point math isn't available in Solidity yet, we adapt the formula for ore wei within the contract . For ships that have not traveled before, the fuel cost for any trip is defined to be ore, for any target. Of the ore proceeds from travel, are burned and are added to the DAO's balance.
Calculator
Disclaimer: this calculator uses JavaScript floating point math, instead of the fixed-point representation that we use in Solidity. As such, the results may be ever so slightly different in-game. Please use this calculator to get a feel for the mechanic, then consult the game UI to finalize your decisions.
Try for The Citadel, for Frontier, for Providence, for Ouroboros, for Outer Ring, and for Abyss. For reference, the maximum map coordinates are .
Ship
Space
Belts
While belts are not a mechanic themselves, they are directly involved in almost every part of the game. As such, they have many associated values, and it is very important that they are defined concretely. Instead of describing the procedure for a mechanic, this section will give a high-level view of the properties of belts and how they are applied.
As game elements, belts have standard coordinates. From here on, will mean the coordinates of belt , or casually, the belt being referenced.
For their limited-resource mechanic, belts have a capacity. This is measured in drill, and is depleted with the sum of the drill of the ships mining there. From here, it will be written as . Internally, a belt's remaining capacity is computed from , the current rate of depletion (in drill per second), , the epoch time of the last change in depletion rate, and , the total capacity depleted prior to the last rate change.
To simulate multiple ores with varying densities, each belt has an optional ore breakdown. This breakdown is not present when the belt is initially added, and is published after the fact by the game developers. An ore breakdown, if present consists of a list of ore multipliers and probabilities for breakdown items . Each controls how much ore a miner receives per second of their operation and the corresponding determines the probability that a miner receives the multiplier when completing their operation. For extra precision, are stored in ore wei and represents a probability of 100%.
The power balance of miners and marauders for each belt is dictated by its transport ship tax and its crime breakdown. Like the ore breakdown, these are both optional and filled upon publication. The transport ship tax dictates the percentage of ore that it siphoned when a miner calls a transport ship to belt . Values range from for zero percent, and for one hundred percent. A crime breakdown consists of a list of theft percentages and probabilities for breakdown items . Each controls what percentage of ore is stolen from a miner's gross claim and the corresponding determines the probability that the theft percentage occurs, should a miner not call a transport ship from . For extra precision, are stored on the same scale as .
To ensure that the developers are unable to manipulate belt publications, each belt is initialized with a provenance value . When the developers send a transaction to publish the belt, the contract verifies that , the value that they submitted when adding the belt. If the hash does not match the provenance, the transaction reverts. This property means that it is impossible for the developers to change the ore breakdown for a belt after adding it, preventing them from manipulating the game based on the interaction that the belt receives.
If mining at an unpublished belt, miners cannot choose the claim option to return to an outpost. Instead, they must forego any rewards by choosing to call a transport ship in order to proceed to another location. This serves as a failsafe, ensuring that assets cannot be locked at unpublished belts.
Regions
Overview
As a way to organize belts with similar crime and transport ship tax rates, the map is separated into regions. From Frontier through Abyss, regions get more distant from The Citadel and present increased risks and rewards. The transport ship tax controls the percentage of ore that is deducted from miners who opt to claim without returning to an outpost. The crime outcomes control the likelihood that 0%, 15%, 30%, 45%, 70%, or 100% of a miner's ore claim is stolen, should they opt to return to an outpost to deposit it. In the case that 100% of a claim is stolen, the claiming ship is also destroyed (burned) permanently. In all regions except for the Abyss, transport ships are considered to be the safe option, as the percentage of ore deducted is always known in advance. However, at distant belts, the increased transport ship taxes and the relatively low chance of destruction may encourage miners to take a risk. In the Abyss, high-value ores are abundant and transport ships are not available at all, meaning that all miners must embrace the odds.
Example Belts
| Shown As | Region | Coordinates |
|---|---|---|
 | Frontier | |
 | Providence | |
 | Abyss | |
 | Ouroboros | |
 | Outer Ring |
Theft Probabilities
| Region | 0% Theft | 15% Theft | 30% Theft | 45% Theft | 70% Theft | 100% Theft |
|---|---|---|---|---|---|---|
| Frontier | 55% | 15% | 15% | 10% | 3.5% | 1.5% |
| Providence | 65% | 15% | 10% | 6% | 3% | 1% |
| Ouroboros | 70% | 12.5% | 7.5% | 5% | 4.2% | 0.8% |
| Outer Ring | 75% | 10% | 5% | 5% | 4.6% | 0.4% |
| Abyss | 77.5% | 5% | 5% | 2.5% | 5% | 5% |
Transport Tax
| Region | Tax |
|---|---|
| Frontier | 25% |
| Providence | 30% |
| Ouroboros | 35% |
| Outer Ring | 40% |
| Abyss | N/A |
Outposts
Outposts are travel targets in the game where returning mining ships can claim their rewards without a transport ship. More on this can be found in the mining rewards section. The Citadel is a special outpost where ships can be staked and unstaked, but other outposts are planned. Information regarding staking is in the staking section.
Mining
Definitions
- - The drill trait of ship (in drill per second)
- - The capacity of belt (in total drill)
- - The th drill multiplier within the ore breakdown of the referenced belt (in ore wei)
- - The density of the th ore within the ore breakdown of the referenced belt (in representation)
- - The transport ship tax for belt (in representation)
- - The theft percentage of the th crime outcome within the crime breakdown of the referenced belt (in representation)
- - The probability of the th crime outcome occurring for non-transport ship claims at the referenced belt (in representation)
Depletion
Each belt's resources deplete with the sum of the drill of its active mining operations. Concretely, each second, a belt 's capacity depletes by for each ship mining at . As ships begin and complete their mining operations, this rate changes. Because it is infeasible gas-wise to store and loop through each rate on every mining transaction, we have to compute depletion a little differently.
Internally, we keep track of belt depletion as , the current rate of depletion (in drill per second), , the epoch time of the last drill rate change, and , the total capacity depleted from prior to the last rate change.
This makes it straightforward to compute the depleted capacity of (in drill) as , for epoch time after . The remaining capacity for is then . The downside is that we lose onchain access to the remaining capacity for times before , but because it is simple to compute from logs and timestamps only move forward on the blockchain, it is no big deal.
When a transaction is sent to start a mining operation for some ship at , we first check . To prevent overdrilling, we compute the belt's hypothetical drilled capacity after a second of drilling at the new rate, . If , it's clear that the belt doesn't have the capacity to support this ship, and we revert the transaction. Otherwise, we commit the depletion at the rate excluding , , note the time of commit , and update the current drill rate to account for the drill of the new ship.
Things get a little more complicated when a stop mining transaction is submitted for a ship at . To start, we check . If , we know that the belt has had the capacity to support 's drill for its entire operation, from its start time to now. In this case, all we have to do is commit the depletion at the rate including , , note the time of commit , and update the current drill rate to account for the removal of 's drill. If , the belt's capacity was depleted somewhere between the start mining transaction for and now. Assuming that , we can compute when by computing how long it took to reach capacity from the last commit, and then adding it to the time of the last commit . This gives us the epoch time of the belt's depletion, .
To ensure that our assumption holds for future exits, we update the rate as normal , but commit the depletion as only the belt's capacity , and set the commit time to the second that the belt was depleted, , instead of the current epoch time. To avoid division by zero when all ships have exited, we use for when .
Rewards
When mining a belt, a miner accumulates rewards in the form of total drill, up until the belt's capacity is depleted. Upon completion of their mining operation, an ore wei per drill value is selected from the belt's ore breakdown, and multiplied by the total drill the miner has accumulated to determine their gross ore owed.
Suppose that a ship has been mining at belt since epoch time . At epoch time , stops mining and requests to claim its rewards. To compute their rewards in ore, we must first compute their operation's total drill. To do this, we first check the drilled capacity of at , . If , the belt hasn't yet been depleted, meaning that the miner's is simply . Of course, if , the belt was depleted sometime before . In this case, we can use , as computed in the depletion section. Thus, we have for the 's total drill.
Aside from the mining operation's total drill, the net ore that receives is dependent on whether its pilot opts to
call a transport ship or return to an outpost themselves. To reduce branch count, the and a boolean indicating
whether the pilot is returning are stored in each case. A random request is then sent through Chainlink's VRF, the result
of which will determine the pilot's fate. If will be returning to an outpost to claim its ore, its travel state is
updated and ore is burnt for fuel according to distance, as usual. It is also marked as Returning at this point, and
forbidden from traveling until it arrives at the outpost.
When the random request is fulfilled with random , it is modulated by our precision basis, . We then select the first such that . This multiplier allows us to find the gross ore of the claim, . If there are no marauders roaming at , this is equivalent to the net ore owed to the pilot, and no further computation is necessary. Otherwise, the remaining process for determining the net ore for 's claim is dependent on whether its pilot has opted to call a transport ship.
If 's pilot has opted to perform the claim by transport ship, the net ore for the claim is calculated as the percentage of the gross ore claim in wei that is not lost to the transport ship tax, . In whole ore, this is .
Otherwise, the crime outcome affecting return is selected through a process similar to that used for the ore wei per drill. We select pick the lowest for which . We then compute the net ore wei owed to the miner, . In whole ore, this is . In the case that , the entire gross ore reward is stolen and is burned.
In reality, this process has to occur in three transactions in order to accommodate per-request randoms. The miner initiates
the process by submitting a transaction to commit their claim. In this step, we store the operation's total drill, 's id,
and whether will be returning. If is returning, we also initiate the travel process, burning the necessary fuel and
marking it as Returning. We then send a random request to Chainlink VRF. When the request fulfills, Chainlink calls into
the game contract, allowing it to store . Once has been stored, the pilot may submit a transaction to
reveal the outcome of their operation, computing and accounting for their net ore.
Calculator
Disclaimer: this calculator uses JavaScript floating point math, instead of the fixed-point representation that we use in Solidity. As such, the results may be ever so slightly different in-game. Please use this calculator to get a feel for the mechanic, then consult the game UI to finalize your decisions.
Belt
Ship
Operation
Roaming
Definitions
- - The attack power of ship (in gun units)
Rewards
Once a marauder ship has arrived at a belt , it may begin roaming there. Roaming grants a portion of the ore siphoned through transport ship taxes and crime outcomes, proportional to the percentage of the belt's attack power that it contributes. In concrete terms, for a claim where ore is stolen, will receive , where is any ship at (including ).
Because it is impractical to compute and update for each marauder each time it changes, we have to store the rewards in a form that allows a single storage update to apply to all marauders. To achieve this, we store , the total attack power at , , the total ore wei to be issued per gun at , and the annulled ore per gun for each marauder ship at . This allows us to keep track of how much ore each marauder is owed, without having to keep track of the rate. We can then compute the ore wei owed to a marauder ship as .
When a marauder ship arrives at and begins roaming, we set and . This correctly starts with zero ore wei owed, and allows us to account for the extra attack power at the belt moving forward. Because only increases throughout the life of the belt, the computation is safe from underflow.
When ore wei are siphoned, it is straightforward to divide it by the total attack power to figure out the increase in ore wei owed per gun . Because ore owed per ship is computed directly from , no additional writes are necessary.
When a marauder ship leaves , note the decrease in total attack power at , , find the ore wei that are owed, , and issue it to 's pilot. For the sake of the gas refund, we also set . Because the has left the belt, will be set properly if it enters again and begins roaming, making the operation safe.
Claiming Ore
All ore gains from ships' mining and roaming operations are mapped to their stakers' addresses and may be claimed at any time through a separate transaction, in compliance with the pull-payment pattern. Because banking state is tied to addresses and not ships, pilots do not lose their pending ore when their ships are unstaked, transferred, or destroyed. When a pilot claims their pending ore, a 2.5% tax is levied and added to the DAO balance, and their remaining ore is transferred to their address.
Construction Bay
Potential for Change
We're actively considering a few changes to the functionality of the construction bay. Information in this section may be updated regularly.
New ships are brought into the game through the ship construction bay, a periodic sealed-bid (blind) dutch auction system. Weekly, all addresses will have one day to bid on a number of ships, with unknown traits. Each individual address may bid on up to 3 ships. Once the auction has completed, all bids will be released, and the winning bidders will be able to claim their ships. Each winning bidder will pay the price of the lowest winning bid.
Because all transactions are publicly visible on the blockchain, sealed-bid auctions are not straightforward to implement. To work around this, we have created a system that allows bidders to show that their bids are valid and commit to them, without revealing the bids themselves. This is possible by leveraging the power of zero-knowledge proofs.
Definitions
- - The time in epoch seconds, in each example
- - The tax on a value , according to the fixed-point tax rate
Auctions
Auctions may only be added by construction bay admins. When a construction bay admin submits a transaction to add an auction, they include the following parameters:
- - The ID of the auction
- - The start time for the auction, in seconds since the epoch
- - The end time for the auction, in seconds since the epoch
- - The reveal period duration for the auction, in seconds
- - The flat tax rate for the auction, in 4-decimal fixed-point representation
- - The no-show tax of the auction, in 4-decimal fixed-point representation
- - The portion of the amount spent on ships that is allocated to governance, in 4-decimal fixed-point representation
- - The portion of the amount spent on ships that is allocated to depositor rewards, in 4-decimal fixed-point representation
- - The ID of the ShipTraits batch used for the auction
- - The ID of the first token issuable from the auction
- - The total number of ships allocated to the auction
- - The address of the ERC20 token contract that will process deposits for the auction
For convenience, let these same definitions apply to the referenced auction for each example in the following sections.
Before adding the auction, we check that:
- Auction does not already exist
- Auction does exist if , meaning is a contiguous ID
- The auction does not end before it starts,
- The auction will not start immediately,
- Participants will have enough, but not excess, time to bid,
- Participants will have enough, but not excess, time for reveals,
- The auction has ships allocated to it
- The flat tax is economically preferable to the no-show tax
- The no-show tax cannot cause insolvency,
- The combined tax on winners cannot cause insolvency,
- The admin has not omitted the auction's token
- No ships from the auction have already been promised
- Trait batch is in the
Readystate and controls at least the ship range
Provided that these checks pass, we associate all the passed parameters with the auction . Beyond the parameters that are used to initialize it, an auction is defined by the following (mutable) state variables, each of which is zero-initialized:
- The deposit, in wei, for a depositor
- The bid, in wei, for a depositor
- The quantity of ships bid on for a depositor
- 1 if depositor has revealed their bid
- 1 if depositor has claimed their auction proceeds
- The Pedersen hash of depositor 's bid ticket
- The total deposit for the auction, in wei
- The total deposit from depositors that have revealed, in wei
- The total revealed bid for the auction, in wei
- The quantity of ships requested by nonzero bidders in the auction
- The winning bid for the auction, in wei
- The number of ships that will eventually be claimed from the auction, determined after the winning bid
- The number of ships claimed from the auction so far
- 1 if governance proceeds have been claimed for the auction
For convenience, let these same definitions apply to the referenced auction for each example in the following sections.
For the sake of simplicity, we will refer to the active auction as "the auction" in each of the following sections.
Standard Parameters
Although the construction bay has been designed to accept auctions with varying tax rates, payment tokens, winning submission delays, and finality delays, these parameters will be constant for the foreseeable future. For the standard auction, we expect the following definitions to hold:
- , 24 hours
- , 5%
- , 50%
- , 30%
- , 10%
States
After it has been added, an auction may be in one of five states at any time: Inactive, Bidding,
Revealing, AwaitingWinningBid, or Claiming. All auctions move through these states in order, and there is
no return to a state once it is complete. An auction will move from Inactive to Bidding,
then to Revealing, to AwaitingWinningBid, and finally to Claiming.
Bidding
When , the auction is considered to be in the Bidding state. During this time, participants
may deposit any nonzero amount of the auction's native token and commit to a bid.
When a depositor sends a commit transaction for the auction, they include the following parameters:
- - The ID of the auction
- - The number of tokens that they will deposit, in wei
- - The number of tokens that will be usable towards their bid, in wei
- - The Pedersen hash of their bid ticket and a secret value that they have generated
- - A PLONK proof that they know a bid ticket that requires at most tokens and, when combined with their secret, hashes to
We start by checking that:
- The participant actually intends to deposit,
- The participant has not already deposited,
- The participant has a valid bid for , provided that is valid,
- The participant's bid ticket and secret aren't already known from their hash
The construction bay then stores its balance , attempts to transfer from the depositor's balance to itself, and records its new balance . It then computes the net deposit increase, , and verifies that at least tokens are truly usable towards bids, .
At this point, it is known that the participant's bid is valid, and the construction bay can update its state to record the participant's deposit and commit:
- Mark as used
Revealing
When , the auction is considered to be in the Revealing
state. All depositors, including those with zero bids or quantities, must reveal their bids during this phase to
avoid the no-show tax. To reveal their bid, a depositor submits a reveal transaction with the following parameters:
- - The ID of the auction
- - Their bid per ship, in wei
- - The number of ships they bid on
- - A PLONK proof that they know a secret that, when hashed with their bid ticket, produces
We start by checking that:
- The participant has deposited,
- The participant has not already revealed,
- The participant has not changed their bid,
We then update the auction's state to note that has revealed:
- If ,
Finally, if has a nonzero bid and quantity, we insert into an auction-specific binary tree of bids times.
It's worth noting that the reveal step is essentially a Pedersen hash comparison, and thus does not require a zero-knowledge proof. However, we have chosen to implement the check as a proof in order to reduce attack surface and simplify the construction bay contract's implementation.
Submitting the Winning Bid
When and , the auction is considered to be in the
AwaitingWinningBid state. During this state, the action available to participants is to submit .
To submit a winning bid, any address may send a submission transaction, including the auction's ID. The construction bay then computes the maximum ships claimable from the auction, .
In the case that , either the auction had no participants, or no participant revealed their bid on time. To ensure that the auction's ships can be used in a future release, we note that there will be no ship claims and ensure that this remains true by setting for all .
Otherwise, if , we select as the th largest bid from the auction's binary tree. We then set .
Depositor Rewards Interlude
Before we move on to the Claiming state, we need to discuss the motivation for and implementation behind depositor rewards.
The point of allowing everyone to deposit into the contract is similar to bluffing in a game of poker: people reading the deposit transactions have to guess whether the depositor is transferring more than their bid into the contract. This ensures that they can't reliably outbid others by reading transaction data. Distributing bid taxes based on deposits, instead of bids, ensures that depositors have economic incentive to bluff, thus securing the privacy of bids.
Depositor rewards are distributed in direct proportion to each participant's deposit. This is done by computing:
- The depositor rewards pool,
- The reward for each on-time participant ,
Because is known immediately after claiming phase and is known at the time of winning bid submission,
is well-defined during the Claiming phase.
For brevity, let this same definition of apply for the auction referenced in the following sections.
Claiming
When and , the auction is considered to be in the Claiming state. During this
phase, participants may claim the ships, refunds, and depositor rewards that they are owed. To claim, a depositor
submits a claim transaction, including the auction's ID.
We start by checking that the participant has deposited and hasn't claimed, , . Next, we check whether the participant was a no-show . In the case that they were, we compute their refund by deducting the no-show tax from their deposit . We then mark that they've claimed and send their refund to them.
If the participant was not a no-show, we compute the number of ships that they won from the auction:
If , the participant was either outbid or too late, and will not receive any ships. We compute the number of tokens they are owed by adding their depositor rewards to their deposit, then subtracting their bid taxes, . We then mark that they've claimed and send them wei.
Otherwise, if , the participant won ships, and the process is more complicated. We begin by computing the number of tokens they've spent on ships, . We then find the portion that is allocated to the depositor rewards pool, , the portion that is allocated to governance, , and the portion that is burned, . Finally, we mark that they've claimed , note their claimed ships, , send them unrevealed ships, burn wei, and send them their refund, wei.
Withdrawing To Governance
At any time during the Claiming phase, anyone may withdraw the auction's governance proceeds to the DAO. To do this,
anyone may submit a withdrawal transaction, including the auction's ID.
The construction bay then verifies that the proceeds have not already been withdrawn, and computes the auction's governance proceeds:
By adding to the governance proceeds in the case that , we ensure that tokens do not get locked in the construction bay. We expect that, if this happens, governance will vote to distribute back to participants.
To finalize the withdrawal, we mark that the proceeds have been withdrawn, and send the wei to the DAO.
Economic Balance
Overview
Our approach to economic balance with The Citadel is focused on maintaining a sustainable ecosystem value by promoting equilibrium between generation and burn of the supply of both ships and ore.
As with any game, there are numerous variables and a large degree of randomness that make it impractical to approach economic calculations directly. We instead took a more objective approach, starting from a point where all players have acted rationally and worked backwards to observe the economic effects. By adjusting the costs and benefits of each game action accordingly, we have established an economic atmosphere in which equilibrium is achieved naturally as the game is played.
After an initial phase of in-house balancing and due diligence, we wanted to go a step further by hiring a third party consulting firm to model and verify our economy. We were the first onchain game to partner with the team at Machinations in comprehensively modeling our economy with their cutting edge technology and professional economic expertise. Machinations utilizes a powerful software tool designed from the ground up to prototype, model, and test game mechanics. Since its inception, Machinations has earned a reputation for massively reducing the time needed to bring new titles and gameplay features to market.
The power of Machinations' software lies in its Monte Carlo simulations. These simulations predict the probability of different outcomes depending on the interaction of random variables, such as player action or skill. The resulting data can be used to assess the impact of risk and uncertainty in prediction and forecasting models for finance, engineering, and supply chain operations.
As of March 16, 2022, The Citadel game has passed the Machinations game economy health verification program.

You can read more about the Machinations partnership here.
As former EVE Online players, we take great inspiration from EVE's economy which likely represents the most sophisticated and longest running virtual economy in existence. EVE's Chief Economist Eyjolfur Gudmundsson took a hands-off approach and let the community decide the value of commodities and goods. The EVE team only intervened when serious exploits or issues posed major threats to the game economy. Taking this a step further, The Citadel places economic control in the hands of an informed community. The team sees this as an important progression in creating a dynamic economy where each independent contribution or action truly matters. We intend to provide adequate economic reports on the state of the game, just as Eyjolfur Gudmundsson's team did for EVE. Our goal is to empower the community to make informed decisions for the future of the game.
Equilibrium
The Auction House and Percentage Based Burn
Refer to Construction Bay for a more comprehensive explanation of the auction house, this section focuses on the overall effect it will have on the game economy.
The weekly auction will contribute the largest ore burn in the ecosystem and does the heavy lifting in curbing inflation. Many onchain game projects set a constant mint value for creating new NFTs, and this linear cost cannot keep up with token inflation. The problem is that it's not possible to burn all ore that is generated without reducing the circulating supply to zero. However, by consistently burning a percentage of tokens generated we see an inflation curve that slopes towards equilibrium. Ore mint value will adjust to the upside naturally over time as more supply is generated and demand increases.
Chart 1
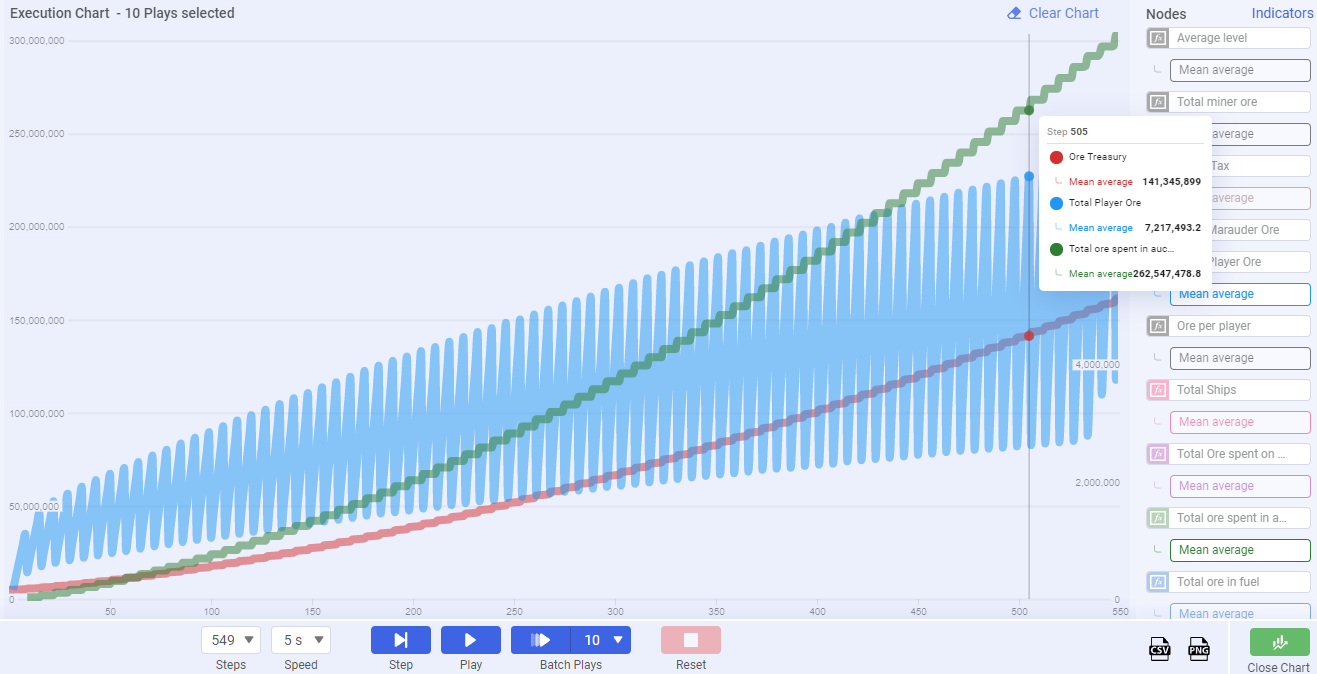
In the above chart, we can see that the auction house is what creates this zig-zag effect on the trend lines. It is a weekly event that causes large fluctuations in the circulating ore supply.
Price Cliffs vs. Dynamic Pricing
The fixed price minting approach in many onchain games employs what is commonly called a "price cliff" method to determine the mint price of new NFTs. After a predefined quantity of NFTs are minted, the mint price denominated in the native token is increased to a new level which essentially devalues the token. Spending power falls off a cliff at regular intervals by design in a misguided effort to combat runaway inflation.
The Citadel Game does not use the price cliff method and new ships cannot be minted at will. Instead, new ships are minted in our weekly auction from the Construction Bay. The price in ore of the ship NFTs will be set by the community via the auctions which results in all "new mints" being priced dynamically. This allows the value to fluctuate as needed to meet market demand and is part of what allows equilibrium to be reached naturally. Due to the limited supply of 3,333 ships at launch, the auction method will likely create a healthy demand for ore as well as an incentive for those outside the ecosystem to enter the game through this avenue.
Chart 2
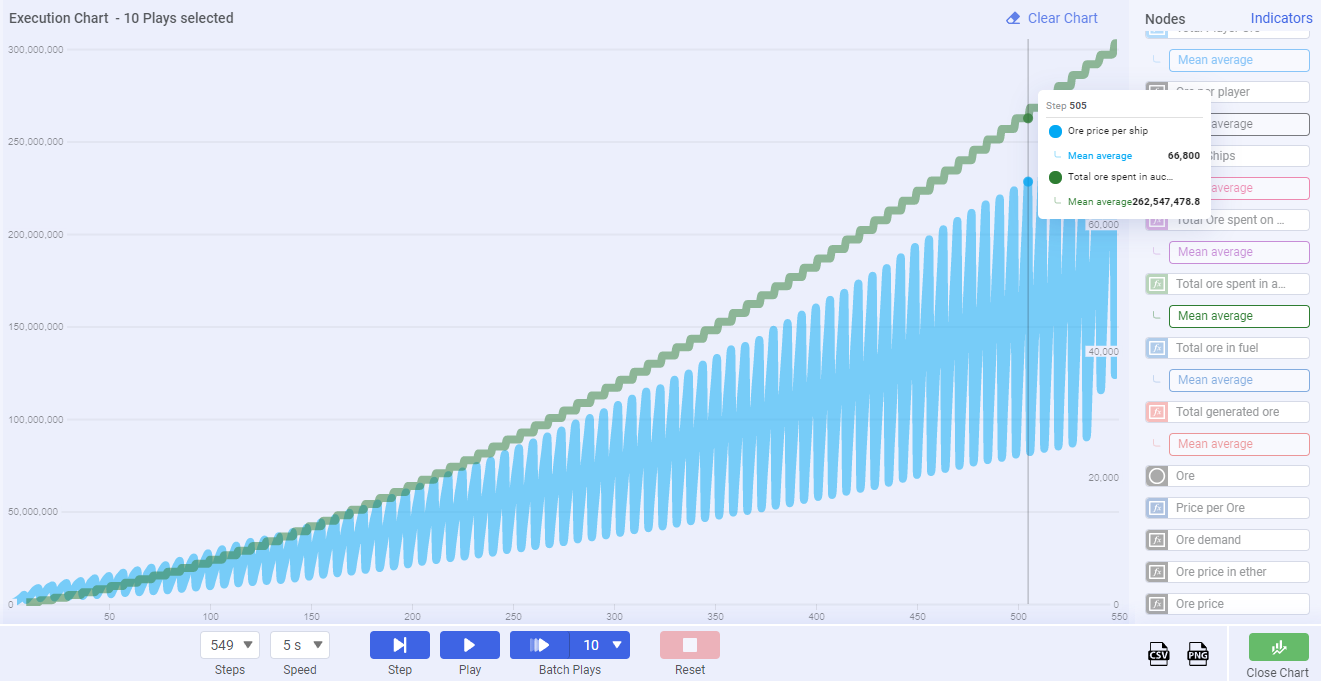
Here we can see the general trend of ship prices over time. Notice that the cost naturally tends to increase as more tokens enter the circulating supply. Keep in mind, these values are simulated and are based on assumptions about demand and that no new game mechanics are introduced. In reality, we will see highly variable market dynamics.
Capturing demand dynamically in the auction house allows the circulating supply of tokens to expand and contract as needed. When ore supply is high then it follows that more auction bids will increase and more ore will be burned. When ore supply is low then we should see lower bid values, resulting in less ore getting burned. As the community creates new gameplay and utility for the ore token, the team expects to see the auction house ore bids shrink to compensate and allow for ecosystem growth.
Chart 3
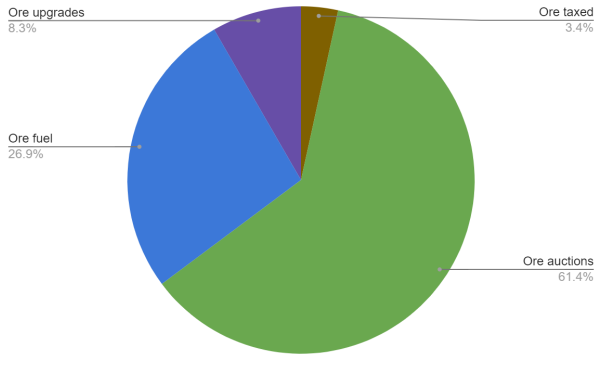
As we mentioned above, ore spent at auctions can increase or decrease as necessary and will depend on a number of variables. This is a healthy relationship because it essentially allows for the circulating supply of ore to be soft capped by player decisions. Beyond the Construction Bay auctions, there are three additional main ore sinks which remain relatively static during gameplay: ore fuel, ore upgrades, and ore taxes.
Ship Destruction
While the dynamic pricing model of the Construction Bay effectively throttles inflation for ore tokens, we also needed to address the reckless inflation of token generating NFTs that plagued many other onchain games. Our first order of business was to find a mechanic that would act as a pseudo-limit on ship inflation. We came up with a novel approach: allow the primary game NFT to be vulnerable to the risk of destruction under certain conditions. Not only does this reduce inflation of the circulating supply of token generating NFTs, it also makes ownership of the NFTs more meaningful in the context of the game world on the premise that we tend to value things more when there's a chance we could lose them.
While it was essential to build this burn into the gameplay, it was also important to the team that the burn risk be optional but well incentivized. With these constraints in mind, we developed the theft and transport ship mechanics as described in the sections on Mining Rewards and Regions. With this approach, players have the option to claim ore safely through transport ships but can also opt for greater rewards by risking a crime outcome. While many crime outcomes involve ore taxes, the greatest risk factor is ship destruction where the claiming ship is burned.
Table 1
| Region Name | Region # | Transport Tax | Chance no Tax | Chance ship destruction |
|---|---|---|---|---|
| Frontier | 1 | 25% | 55% | 1.50% |
| Providence | 2 | 30% | 65% | 1% |
| Ouroboros | 3 | 35% | 70% | 0.80% |
| Outer Ring | 4 | 40% | 75% | 0.40% |
| Abyss | 5 | N/A | 77.5% | 5% |
(Truncated from theft probabilities)
As shown in Table 1, the chances of both ship destruction and 0% taxes increase along with the transport ship tax as regions become more distant. This combination incentivizes choosing the risky option in more dangerous regions where rare ore types are available and ore generation potential is greater overall.
This ship inflation control method acts as a stimulus to the entire ecosystem by increasing ship scarcity, decreasing token generation, and burning ore dynamically based on current demand for ships. We've seen mechanics such as stealing NFTs in many onchain games. However, having an NFT stolen ultimately feels just as bad as having it burnt. Meanwhile, transferring an NFT from one player to another doesn't contribute to inflation control since the NFT that generates tokens still exists. We believe our approach is significantly healthier for the economy and will eventually contribute to reaching an equilibrium supply of ships.
Chart 4
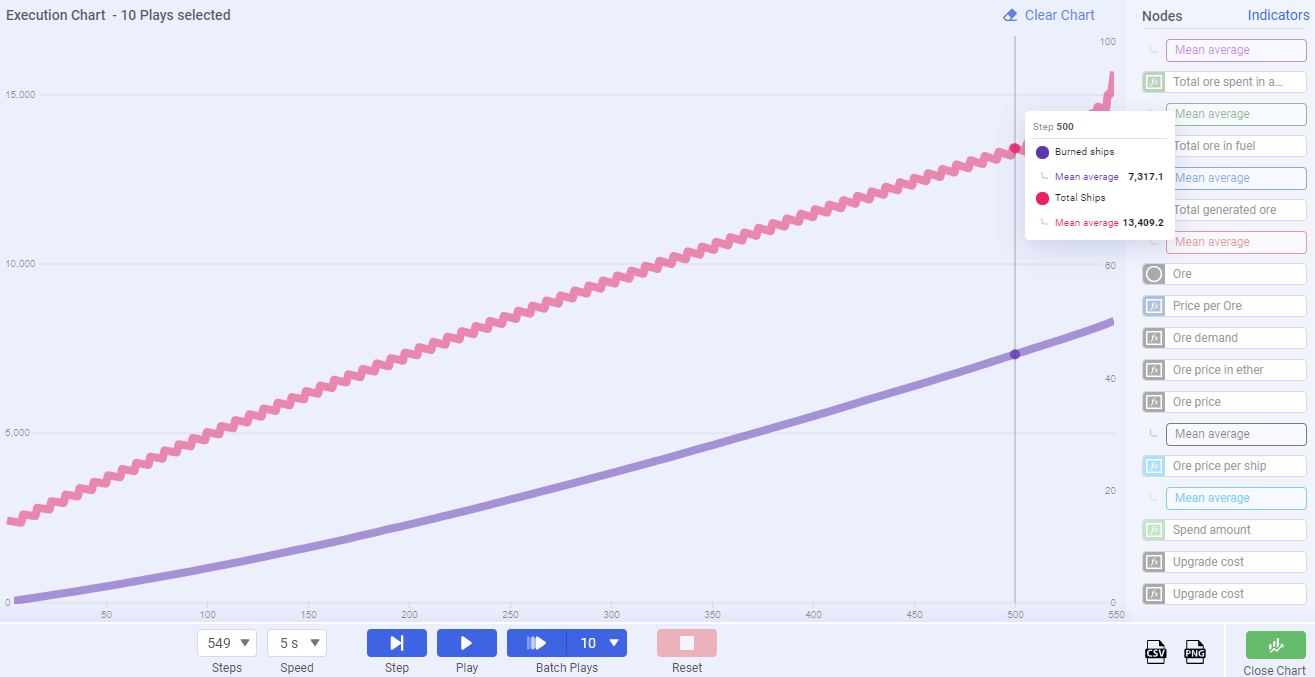
The above chart is based on the simulated results of 500 days of gameplay, where the red line denotes total ship supply and the purple line represents burned ships. The most important takeaway we gleaned from simulating these results is that new ship supply introduced each week will eventually be equal to the amount of ships burned each week. This will likely fluctuate and would take years to occur, but it is important to demonstrate that the tendency towards equilibrium is built into the mechanics of the game. The important thing is that these two lines slope toward one another and will eventually converge in equilibrium.
The reason that these two lines converge is because ship supply increases are semi-linear and will predictably fall within a narrow range of new ship quantities offered at auction. Meanwhile, ship destruction will tend to be a percentage based burn of the total supply. As total supply increases, total ship burns will increase until they are relatively equal to the number of new ships introduced at auction.
Disclaimer: Any charts inserted into this document are from the Machinations model. It's important to note that these simulations are based on imperfect information as there is no direct statistics to input into the models. The trends in the simulations inform us that the mechanics and overall economic design should be sustainable. These models will be updated with inputs from the blockchain once the game goes live so that we can more accurately monitor the game economy health.
Upgrade Balance
In the short to medium term, ship upgrades are intentionally cost-inefficient in terms of the immediate increase in ore generation for miners. Because marauder yield is balanced against that of other marauders, ship upgrades will be necessary in order for marauders to maintain sufficient attack power to compete with their peers. We've attempted to balance the increased stats of more powerful ships by increasing their upgrade costs proportionally. This way, the immediate benefit of generating more ore is balanced by the increased cost of upgrades. As equipment is introduced to the game, upgrade tiers will become very important. Although initial upgrades for miners may be cost-inefficient, they will gain access to higher-powered equipment in the future.
That upgrades are inefficient for miners and necessary for marauders is itself a form of balance. Inefficiency for miners means that the cost of upgrading a ship's power to the maximum is great enough that the corresponding gain in yield will take over 60 days* on average to pay for itself. In this way, miner upgrades decrease the available supply of ore in the short and medium term. Meanwhile, marauder upgrades do not increase the ore supply and have an overall deflationary effect since the ore cost is burned.
In most onchain games, the standard effect of upgrades is a linear boost to utility token generation which can inadvertently cause more inflation. To avoid this, we've designed the system to be nonlinear as described above. Overall, we consider the upgrade utility for The Citadel to be a deflationary mechanic.
*Upgrade costs in $ORE for miners have been reduced across the board. Training time costs have been greatly reduced for both Miners/ Marauders.
Work, Weight and Multiplayer Effects
In our effort to create a robust economy it was important to design the game such that each decision carried real weight. With this in mind, the team developed a fully onchain real time player positioning system based on a 2D star map. There is a cost in both ore and time to travel across the map and earn resources. Consequently, each decision requires meaningful strategic consideration in order to optimally decide where to mine or roam. An economy where tokens are gained without effort or possibility for failure cannot be sustained. Without losers, there can be no winners.
The star map allows for multiplayer decision making. A real game economy cannot be created from intertwining a grouping of single player instances. In order for a market economy to flow there must be real competition between players in the same ecosystem. Each ship position may be viewed via the in-game interface and decisions will be based on the distribution of miners and marauders across different asteroid belts in your region. Miners will look for belts that have the best multipliers and fewest miners. Marauders will look for belts with numerous miners and few marauders. In the weekly auctions, you will be bidding against other players rather than minting at a linear cost. This inherent multiplayer competition is at the heart of what drives a real living, breathing economy.
In Summary
We have taken great care and utilized every resource at our disposal in designing a state of the art, robust and sustainable onchain game economy. Throughout this process we were guided by the holistic philosophy that for an onchain game economy to work it had to be founded on the same core principles as any real economy. The aim was to lay a sturdy foundation for a long lived game world we co-create along with the community.
Bridging
Overview
In The Citadel, gameplay and governance happen strictly from layer 2, and yet we expect most item trading to happen on layer 1. In order to make ships and ore natively accessible from both networks, we've instituted a bridging system to connect state on both layers, inspired by EtherOrcs' portal and castle system, and written over FxPortal.
At a high level, this system involves two tunneling contracts. Each tunnel exposes a send function to set of privileged contracts (i.e., parts of the game). When a contract on layer 2 needs to make a call to one on layer one, or vice versa, it encodes the function call data, along with the address of the target on the receiving network, and sends it to the tunnel.
Through Polygon's StateSync mechanism and FxPortal, the tunnel on the sending layer sends the encoded call data to the
receiving network. Once the tunnel on the receiving network receives the message, it executes each call, as was desired
by the sending contract on the sending network.
The receipt process happens automatically and quickly (usually within 10 to 15 minutes) from layer 1 to layer 2, where each state sync is pushed individually by network miners. From layer 2 to layer 1, transfers are slower due to an extra verification period, but usually process within 30 minutes to 3 hours. Because transactions into layer 1 must use constant data, a cryptographic representation of the set of transactions is pushed, and users must prove inclusion and push their transactions through themselves. Fortunately, The Citadel automates the proof process, and pilots will receive notifications in their hangars once their ships have been processed.
In order to maintain security while keeping simplicity, security is handled directly by each network's tunnel, which verifies that the message was sent by tunnel on the opposing network. It is then guaranteed that any calls from the tunnel on each network were originally dispatched by a valid sender from the opposing network. For additional assurance, privileged governance calls coming from layer 2 to layer 1 are passed through a separate tunnel. This allows the standard tunnels to maintain minimal privileges, while still allowing governance complete control over the project.
Though it may sound complicated, this system of bridging has a major benefit: aside from the tunnels and their privileges, all contracts can remain identical across networks. This allows for faster development with fewer footguns, reduces the amount of code that must be tested and audited, keeps our surface area for attacks smaller, and, most importantly, allows community builders to gain an understanding of the system with less effort.
Docking
Docking is the process by which ships are transferred between networks. As is standard with bridging ERC-X tokens, the goal is to burn the token on the sending network and reissue an identical one on the receiving network. In order to keep gas usage low, we simulate this by transferring the ship to the contract and either issue or update it on the receiving network, depending on whether it already exists there. This maintains the condition of keeping the token inaccessible on the sending network, without incurring the gas fees associated with ERC721 mints on the receiving network.
When a pilot docks a ship on the sending network, the dock/bank contract simply transfers the ship to itself then requests a call to its own undock function, which issues or updates the token on the receiving network, transferring it to the pilot.
Banking
Banking is the process by which ore is transferred between networks. Like docking, it works by rendering the banked tokens inaccessible from the sending network, then issuing them on the receiving network. Because balance tracking is made simple by ERC20, tokens are always burnt on the sending network and minted on the receiving network.
When a pilot banks ore on the sending network, the dock/bank contract simply burns the ore being sent, then requests a call to its own unbank function, which mints ore to the pilot on the receiving network.
Governance
To put the game in the hands of the community, The Citadel will be controlled through an onchain governance system,
built over OpenZeppelin's Governor, Timelock, and ERC20Votes bases. These expose a set of functions for submitting
proposals, allowing pilots to vote on them, and automatically executing the effects of the proposals that pass.
For each ship staked, a pilot may claim one pilot's badge. For each ship unstaked, one of the unstaking pilot's badges will be burnt. Each pilot may cast one vote per pilot's badge per proposal, and pilots with 5 or more pilot's badges will automatically be granted proposing privileges. To prevent manipulation of the badge supply during voting periods, each pilot's badge holdings, as well as the total badge supply, are checkpointed at each change and each proposal uses the last snapshot before the vote is initiated.
Pilot's badges are ERC20Votes tokens, modified to prevent transfers and approvals, except by authorized contracts.
This ensures that pilot's badges are locked to staked ships, and that governance shares will not be treated as a commodity
to be bought and sold on their own.
Emergency Multisig
While it is extremely important that the governance system retain ownership of all of the contracts, its voting period and execution delay make it impractical for emergency updates. To avoid this problem in the case that there is an emergency, we have created a multisig, and given it the necessary privileges to upgrade non-governance contracts without the need for a DAO vote.
Although the governance system can revoke these privileges permanently through a vote, this is still a point of centralization. In order to ensure that these privileges are used only when necessary, we have included the entire core team, select community members, and the Machinations team (a third party) in the multisig. Each party will have their own multisig with majority participation required in order to use the emergency multisig for transactions, as an added protection against key loss. This means that, if the emergency multisig were to be used, the core team, the additional community members, and Machinations as a company would all have to back it, with their reputations as collateral.
It is our belief that these consequences are severe enough to prevent abuse. If the community believes otherwise, we will gladly hear a well-considered proposal to remove the emergency multisig.
Handoff
After all contracts are deployed, but prior to launch, The Citadel team will relinquish control over upgrade permissions, as well as all contracts' admin roles, giving full control to the community through the governance system. Practically, this means that The Citadel team will retain only the roles necessary to add belts, publish belts, and improve gameplay, while still allowing the governance system to revoke each of these permissions (and not vice versa).
In more technical terms, this means that the governance authority for each network will be the sole admin owner of its
ProxyAdmin, but that The Citadel team will retain proxy admin permissions for the Game, Ore, and Ships contracts.
Similarly, the one and only address with DEFAULT_ADMIN_ROLE and TIMELOCK_ADMIN_ROLE will be the
governance authority, but The Citadel team will retain ADDER_ROLE, PUBLISHER_ROLE, CONSTRUCTION_ADMIN_ROLE, and SHIPS_UPLOADER_ROLE.
This system works analogously to a token approval, allowing The Citadel team to upgrade Game, Ore, ConstructionBay, ShipTraits and Ships, but
preventing it from giving itself extra permissions and allowing the existing permissions to be revoked at any time. If
the community so chose, The Citadel team could have its upgrade permissions removed immediately, and any upgrades it made
could be reverted.
Proposing
Proposals consist of a unique identifier, a human-readable description, and a set of encoded function calls to execute if the proposal is executed. The unique identifier is used for vote tracking, the description serves as an onchain record of the pitch to voters, and the function calls determine the concrete effects of executing the proposal.
Casting Votes
Pilots may cast votes for each proposal, either in favor of the proposal, against the proposal, or abstaining from the proposal altogether. While the first two stances are self-explanatory, abstaining is also significant, in that it helps a proposal reach quorum, while signaling stakeholder has no opinion on it.
When casting a vote, it is extremely important that pilots ensure that id of the proposal that they are voting on matches the id of the proposal that they read. We will do our best to suppress spam, but, by design, it is impossible for us to censor proposals coming from the community.
Executing Proposals
In order to execute a proposal, two things are required: quorum must be reached, and the majority of votes on the proposal are in favor. If quorum is reached, but the majority of votes are not in favor, the proposal is rejected and will not be allowed to execute. However, if both requirements are met, the proposal is set to be available for execution after a set delay.
This delay is set initially by the project owners and adjustable by the governance system itself. It is enforced by the timelock, which serves to allow stakeholders who voted against the proposal a chance to exit the project before the proposal's execution. Once the delay period has passed, anyone can execute the passed proposal.
Executing Proposals That Require Bridging
Executing passing proposals on layer 1 from layer 2 requires use of the governance tunnel, the behavior of which is outlined in the bridging section. These types of proposal executions are almost exactly the same as normal executions, and the only difference is the required interaction with the layer 1 pull system for execution to complete. Concretely, once the timelock period has passed, the proposal has been executed on layer 2, and governance calls have reached layer 1, an account must prove their inclusion to finalize their execution on layer 1. Because each pilot who voted affirmatively had an interest in seeing the proposal executed, and because any address may complete the execution, it is expected that all valid layer 1 effects will be executed. This assumption is equivalent to that of the propose-execute cycle that has been battle-tested through other DAOs, such as COMP and AAVE.
Veto Power
In order to ensure that proposers have done their due diligence, and that passing proposals will not cause damage to the economic balance or security of The Citadel, the core team will retain a relinquishable veto power at launch. In order for a proposal to be vetoed, its vote must have passed, and it must be queued for execution. Further, the veto must be submitted by the core team's multisig, with 51% required participation.
In order to prevent abuse of the veto power, there is a single proposal for which the veto function is disabled: the pre-written proposal that removes the team's veto power. In the case that the community believes that the team has incorrectly vetoed a proposal, they may vote to remove the team's veto power, then resubmit the original proposal.
We will release the full transaction data for the veto removal proposal within our community resources on the DAO.
tl;dr: The team has reserved the right to veto a proposal considered substandard or harmful to the game or community. The majority of the team must vote in favor for it to take effect. The community can submit a pre-written proposal to remove the team's veto power any time, and this special proposal is immune from the team veto power.